Assignment 2 -- Introduction to Python

Basic Python

• Learn how to perform simple operations such as exponents (Eg:$2^3$), remainder, integer division. Also understand the order of such operations that Python enforces. Run (5-1)*(7+1)/(3-1) in Python interpreter and indicate the order of evaluation of expressions (Note: an expression consists of values and operators such that they can always evaluate to a single value).

• Learn how values of common datatypes such as int, floats, string, and bool are specified in Python by using the interpreter. Interpret the results of the following expressions: (i) 'Python' + 'Rocks' and (ii) 'Python' + 42. Experiment with other combinations of operators and types.

• Variables are named locations in computer’s memory that can store a single value. If you want to use the result of an evaluated expression later in your program, you can save it inside a variable.

  

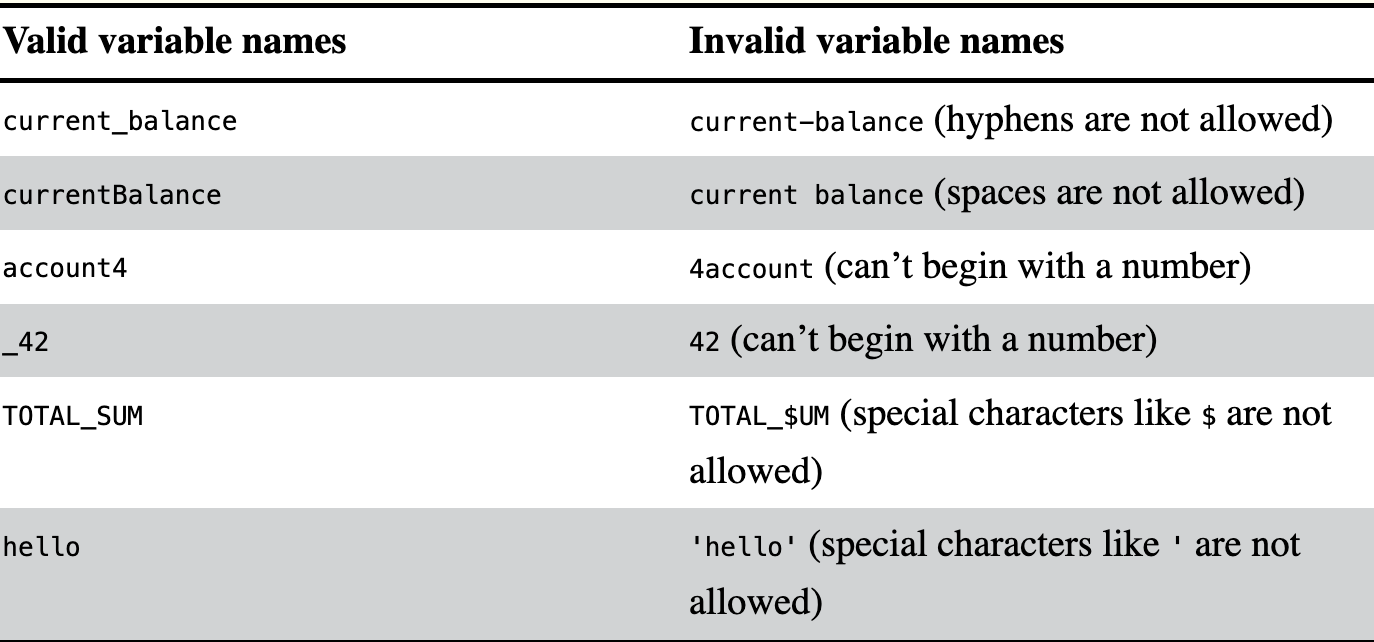
  • Learn the use of print() and input() functions.
    Write a python program that takes as input a float radius of a circle and prints its perimeter and area.
  • Use format() function to print the value of $\pi$ rounded
    to 14 digits.
  • (Conditions) Learn python’s way of specifying conditional
    expressions (if-else, if-elif-else). Given any integer $y$ denoting a year in the Christian calendar, we would like to determine whether it is a leap year. A leap year is one which is divisible by $4$. Also not all years divisible by $4$ are leap years. Century years are leap only if they are divisible by $400$. So we define a boolean function leap which yields a value “true” if the year $y$ is a leap year and false otherwise. Write a python program for the problem above.

• Show in the interpret the output for the following expressions when evaluated:

  • (5 > 4) and (3 == 5)
  • not (5 > 4)
  • (5 > 4) or (3 == 5)
  • not ((5 > 4) or (3 == 5))
  • (True and True) and (True == False)
  • (not False) or (not True)

Basic Algorithm Design and Python Programming

• Computing factorial of a given integer using recursive procedure which is technically complete. For some inputs (from the domain of Integers) the computation may not terminate. Identify such inputs and provide reason for this non-termination.

• Computing $x^n$ through a recursive procedure. Provide correctness and time complexity arguments as comments in the program. Further design and implement a faster recursive version of the power function.

Challenge Question

• The integer square root of $n$ is the integer $k$ such that $k^2 \leq n < (k+1)^2$. The integer square root can be computed using the following inductive process:
  • Compute the integer square root $i$ of $m = n ,\mbox{div}, 4$ recursively. We then have that $i^2 \leq m < (i+1)^2$.
  • Since $m$ and $i$ are integers we have that $(m+1) <= (i+1)^2$. We thus have $(2i)^2 \leq 4m \leq n < 4m + 4 \leq (2i + 2)^2$. Hence we have that the integer square root of $n$ is either $2i$ or $2i+1$.
  • Write a recursive python program corresponding to the above
    algorithm.
  • Derive the number of steps required.